gallorob projects' blog
A blog where I blab about projects & stuff
Project maintained by gallorob Hosted on GitHub Pages — Theme by mattgraham
Paper notes: Evolving Players for an Ancient Game: Hnefatafl
Author: Philip Hingston
Full paper: here
tl;dr
The author explores the possibility of evolving a neural network for evaluating board states of Hnefatafl in order to judge different variants.
The game: Hnefatafl
Hnefatafl is a zero-sum, asymmetrical board game of origins uncertain (find more at the excellent Damian Gareth Walker’s blog). There are multiple known variants, but the one implemented is similar to historical Hnefatafl; in particular:
- the game is played on a 11x11 board
- the attacker has 24 pieces (not 26 as written on the paper)
- the defender has 12 pieces plus the king
- the formation is 12:24 diamond
- all pieces move orthogonally until they reach an edge of another piece (or, for all pieces except the king, the throne or any of the corners)
- a piece is captured by enclosure on two opposite sides (except the king, which needs to be surrounded on all sides)
- the attacker starts first
- the defender wins if the king reaches any of the corners
- the attacker wins if the king is captured; note that the king can be captured also when next to a corner or on an edge Additionally, the following rules have been added:
- if a player has no legal moves, he lose
- after 100 moves, the game ends in a draw
Due to the asymmetrical nature of the game, a player is declared winner after playing two rounds, first as attacker and then as defender. Captures counts are used to break ties.
The evolution algorithm
The evolution algorithm used is a population-based Evolution Strategy. Each player in the population has its own evaluation function, described by the parameters of a neural network. The goal is to obtain a player that chooses the best move to play via a game-tree search, where the value of the board state is predicted by the evolved neural network.
The pseudo-code for the algorithm is:
The fitness for each player was computed as the sum of of the averages of points accumulated playing against every other player and playing 10 matches against the random player. Due to the large branching factor, the game-tree search during evaluation ran at depth 1.
The author notes the problem of stagnation and how it can be prevented by using larger populations. Whenever this is not possible, like in this case, a different way to alleviate such problem is to introduce a Random Player (who plays legal moves randomly) to collect an always-increasing amount of game samples.
The author also notes how the fitness function, due to its noisy nature, may not always return the fittest individual.
The neural network
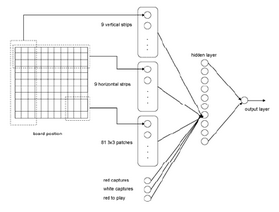
A quick note: the paper is old considering how much has changed in the world of neural networks, so it comes as no surprise that the neural network here implemented is… well, let’s just say that it’s very simplistic and definitely wouldn’t be implemented nowadays. However, it is cleverly designed: the input layer has 1 neuron for each cell (where each cell has a different value depending on what it contains). The next layer contains 3 groups of spatially defined neurons and three additional neurons. The formers contains one neuron for each vertical strip of 3 columns, one for each horizontal strip of 3 rows and a last one for each 3x3 patch of cells. The latters are activated by the number of captures of the attacker, the defender and the turn (one-hot encoded), respectively. Next, the hidden layer contains only 10 neurons, fully connected to the previous layer, and one neuron as output layer (fully connected as well).
Conclusions
The author succesfully shows that ES can indeed be used to obtain a board evaluator with little to no domain knowledge, though the tree search results at different plies raise some concerns. Funnily, no data augmentation for the board states seems to have been used, which could have saved quite a lot of computation time, given the symmetrical nature of the board. Finally, if someone was to redo this experiment, a smarter network architecture would be very similar to the main bulk and the value head of the AlphaGo model (ie: use convolutional layers and residual layers to process the board in a high-dimensional representation).